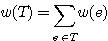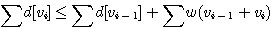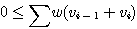제 1 절 소개
정의
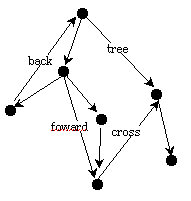
Directed Asyclic Graph(DAG): 사이클이 없는 digraph
edge들의 종류
제 2 절 탐색
넓이 우선 탐색
- queue에 모든 adjacent node들을 집어넣어 가면서 넓이순으로 탐색. 시작노드로부터 등고선이 생긴다.
깊이 우선 탐색
- 등고선이 생기지 않는 반면 recursive하게 호출하기 좋다.
제 3 절 Topological Sort
정의
G=(V,E)가 DAG일 때, i에서 j로 가는 edge가 존재하면, i를 j의 앞에 두는 정렬을 말한다.
알고리즘
Topological-sort(V) mark[v]=visited; for ∀w∈L(V), 단 L(v): adjacency list of v if(mark[n] = unvisited) Topological-sort(w); output v;
위의 알고리즘은 topological order의 역순을 리턴한다.
제 4 절 Strongly Connected Component
정의
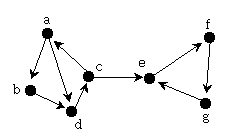
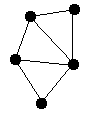
G=(V,E)가 digraph일 때, 모든 vertex들이 서로 연결되어 있는 vertex들의 집합을 G의 Strongly Connected Component라 한다.
어떤 digraph가 단 하나의 strongly connected component로 이루어져 있을 때 그 digraph는 strongly connected되었다고 말한다.
위의 그래프에서 {a,b,c,d}와 {e,f,g}가 strongly connected component이다.
알고리즘
Strongly-connected-component(G) 1. 모든 edge들을 역방향으로 한 Graph을 GR이라 하자. 2. G에 대해 DFS를 호출하여 level을 저장한다. 3. 가장 level이 깊은 vertex에서 GR을 다시 호출한다. 만일 모든 vertex를 방문하지 못하면, 남은 vertex 중에서 가장 level이 깊은 곳에서 다시 DFS를 호출한다. 4. 3에의해 생성되는 tree가 strongly connected component이다.
claim
v와 w가 strongly connected component ⇔ v와 w가 3의 DFS forest에서 같은 tree에 있다.
제 5 절 Minimum Spanning Tree
정의
G의 subgraph 중 모든 vertex들을 포함하는 tree를 spanning tree(MST) T라고 한다.
이 때 spanning tree T의 weight는
spanning tree 중에 가장 weight가 작은 것을 MST라고 한다.
Graph에서 MST를 찾는 것은 각각의 individual을 연결하는 network을 어떻게 만드는 것이
가장 싼 값인가를 구하는 것을 의미한다.
기본 성질
(S,V-S)를 vertex들의 bipartition이라 하자. 만일 {u,v}∈E가 S와 V-S를 연결하는 edge들 중 가장 작은 weight을 가진 edge라면, {u,v}를 포함하는 MST가 존재한다. 즉, MST를 생성하는 알고리즘에서 e를 포함하는 것은 언제나 safe하다.
증명: 어떤 MST T가 {u,v}를 포함하지 않는다면, u,v사이에 다른 경로가 존재할 것이다. 그 경로는 S와 V-S를 가로지르는 적어도 하나의 edge는 포함할 수밖에 없고, 그 경로를 {x,y}라 하면, w({s,y})≥w({u,v})이다.
만일 w({x,y})>w({u,v})이면, T+{u,v}-{x,y}가 T보다 weight이 작기 때문에, T는 MST가 아니다.
만일 w({x,y})=w({u,v})이면, T+{u,v}-{x,y}는 T와 같은 weight을 가지고 있으므로 둘 다 MST가 된다.
이 성질에 의해 만일, weight이 모두 다른 값이면, Graph는 단 하나의 MST만을 가지게 된다.
증명: weight이 모두 다른 그래프가 두 개의 MST T1, T2를 가진다고 가정하자. 이들 Tree가 둘 다 포함하고 있는 edge들이 있을 것이고, 서로 차이나는 edge들이 있을 것이다. 공통된 부분만을 모아놓은 Tree를 T3라고 하자. 이 T3에 포함된 vertex 집합을 V1, 포함되지 않은 vertex 집합을 V2라 하자. T1과 T2에는 V1과 V2를 연결하는 edge들이 하나씩 존재하여야 한다. 그리고 이들의 weight은 서로 달라야 한다.(가정에의해)
그런데 MST를 위한 기본 법칙에 의하면 두 vertex 집합을 연결할 때, 최소 weight인 edge를 선택하는 것만이 safe하다. 그러므로 T1과 T2 중 하나는 MST가 아니다. 증명끝.
Kruskal's 알고리즘
기본 아이디어: 사이클을 만들지 않는 minimum edge들을 더해간다. greedy algorithm이다.
- T = {}
- adjoint set을 root vertex를 포함하도록 초기화한다.
- edge들을 weight 순으로 sort한다. heap을 이용한 min queue를 사용하는 것이 일반적이다.
- T가 |V|-1개의 edge들을 가질 때 까지
- {u,v} = deleteMin(q)
- u와 v가 다른 set에 속해 있는지 판단한다.(adjoint set을 쓰면 log|V|내에 가능) 만일 그러하면: T = T+{u,v}, u와 v가 속한 set을 merge한다.
running time은 P(|E|log|V|)이다. 이것은 sorting과 같다.
Prim's 알고리즘
기본 아이디어: 한 개의 vertex씩 추가해가면서 현재의 MST를 구한다.
- Q = V; // Q는 MST에 속하지 않는 vertex를 말한다.
- foreach u∈Q
- d[u] = ∞
- d[r] = 0; // r : root node, chosen at random
- while Q!={}
- u = deleteMin(Q)
- foreach v∈L(u)∩Q
- w(u,v)
- d[v] = w(u,v); // relaxation
- rebuild priority queue w.r.t. v; //percolation
- w(u,v)
running time은 P(|E|log|V|)이다.
제 6 절 Single Source Shortest Path
정의
digraph G=(V,E)에 대해서, W:E→R을 weight function이라 하자.
- (u,v)가 E에 속하지 않으면, w(u,v)=∞이다.
- 만일 u에서 v로 가는 directed path가 존재하지 않으면, shortest path의 weight은 ∞이다.
- w(u,u)=0이다.
P를 e1, e2, e3, ..., ek를 포함한 path라 하면,
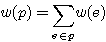
가장 작은 w(P)값을 가진 path로 정의하며, δ(u,v)로 표시한다.
Dijkstra's 알고리즘 - Nonnegative weight를 가정
핵심 아이디어: Prim's 알고리즘과 똑같다. 초기치로 d[v]를 δ(s,v)로 둔다. 모든 vertex에 대해서 relaxation하면서 현재까지의 shortest path를 구한다.
- Q = V; // Q는 MST에 속하지 않는 vertex를 말한다.
- foreach u∈Q
- d[u] = ∞
- d[r] = 0; // r : root node, chosen at random
- while Q!={}
- u = deleteMin(Q)
- foreach v∈L(u)∩Q
- d[v]>d[u]+w(u,v)이면
- d[v] = d[u]+w(u,v); // relaxation
- rebuild priority queue w.r.t. v; //percolation
- d[v]>d[u]+w(u,v)이면
Correctness Proof는 math induction을 이용한다.
Running Time은 Prim's 알고리즘과 같은 O(E log|V|)이다.
Bellman-Ford 알고리즘 - No Negative Cycle를 가정
- d[s]=0
- foreach v∈v-{s}
- d[v]=∞
- for i=1 to |V|-1
- for each (u,v)∈E
- d[w] = min{d[w], d[u]+w(u,v)}
- for each (u,v)∈E
- for each (u,v)∈E // negative cycle check
- if d[v]>d[u]+w(u,v) then "negative cycle"
Running Time은 O(|V||E|)
만일 cycle v0, v1, ..., vk(vk=v0)이 존재하는데 "negative cycle"이 리턴되지 않았다면,
Linear Algorithm - DAG를 가정
- vertex를 topological sort한다.
- d[s]=0;
- for each v∈v-{s}
- d[v]=∞
- for each u∈V in topological order
- for each v∈L(u)
- if d[v]>d[u]+w(u,v) then d[v] = d[u]+w[u,v];
- for each v∈L(u)
Running Time O(|E|)이다. 이 알고리즘은 longest path 알고리즘으로 사용할 수 있다.
제 7 절 All pair Shortest Path
정의
모든 pair간의 shortest path를 구한다.
Floyd 알고리즘
사실 Transitive Closure에서 Warshall이 사용한 방법을 빌린 것이다.
for(int i=0; i<|V|; i++) for(int j=0; j<|V|; j++) d2[i][j] = g.e[i][j]; for(int k=0; k<|V|; k++) for(int i=0; i<|V|; i++) for(int j=0; j<|V|; j++) if(d2[i][j] >d2[i][k]+d2[k][j]) d2[i][j] = d2[i][k]+d2[k][j];
이 알고리즘은 O(|V|3)의 running time을 갖는다.
제 8 절 Transitive Closure
때때로 우리는 distance값은 상관없이 i에서 j까지의 경로가 존재하는가 만을 원할 때가 있다.
Warshall's 알고리즘
int i,j,k; for (i=0; i<|V|; i++) for (j=0; j<|V|; j++) A[i][j] = w[i][j]; // 만일 edge가 존재하면, 경로가 있는 것임 for (k=0; k<|V|; k++) for (i=0; i<|V|; i++) for (j=0; j<|V|; j++) if (!A[i][j]) A[i][j] = A[i][k] && A[k][j];
이 알고리즘은 하나의 vertex씩 더해가면서 계산한다.
sparse graph에서는 Edge에 대해서 계산할 수 도 있다. {u,v}가 더해졌을 때 다음과 같이 update된다.
Ak[i,j]=Ak-1[i,u] && Ak-1[v,j]
O(|V|3)의 running time을 갖는다.
'IT_Architecture > 자료구조 · 알고리즘' 카테고리의 다른 글
| [펌_java를 이용한 자료구조] 재귀(Recursion) (0) | 2007.07.02 |
|---|---|
| [펌_java를 이용한 자료구조] 트리(Tree) (0) | 2007.07.02 |
| [펌_JAVA를 이용한 자료구조] 큐(Queue) (0) | 2007.07.02 |
| [펌_JAVA를 이용한 자료구조] 스택 (Stack) (0) | 2007.07.02 |
| [펌_자바를 이용한 자료구조] 연결 리스트(Linked List) (0) | 2007.07.02 |